Qiiz Review Form G Exponential Growth and Devay

7.1: Exponential Growth and Decay Models

1. Last updated

2. Save as PDF

Page ID

40176

Learning Objectives

In this department, you volition learn to

• Compare linear and exponential growth.
• Recognize and model exponential growth and decay.

Prerequisite Skills

Earlier you get started, take this prerequisite quiz.

1. Simplify \(3(2)^3\).

Click here to check your answer

\(24\)

If you missed this trouble, review hither and scroll to Example 4. (Notation that this will open a different textbook in a new window.)

2. Simplify \(-v(3)^2\).

Click hither to bank check your respond

\(-45\)

If you lot missed this problem, review here and scroll to Example 4. (Annotation that this will open a different textbook in a new window.)

3. Solve \(2^x=xvi\).

Click hither to check your answer

\(x=iv\)

If you missed this trouble, review here. (Note that this will open a different textbook in a new window.)

four. Graph \(y=-\dfrac{1}{ii}x+3\).

Click here to check your answer

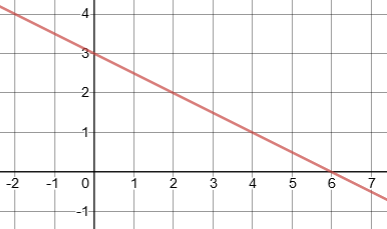
If you missed this problem, review Section 1.two. (Notation that this will open in a new window.)

Comparison Exponential and Linear Growth

Consider two social media sites which are expanding the number of users they have:

• Site A has ten,000 users, and expands by adding 1,500 new users each calendar month
• Site B has 10,000 users, and expands by increasing the number of users by 10% each calendar month.

The number of users for Site A can exist modeled as linear growth. The number of users increases by a abiding number, 1500, each month. If \(x\) = the number of months that have passed and \(y\) is the number of users, the number of users later on \(x\) months is \(y = 10000+1500x\). For site B, the user base of operations expands by a abiding percentage each month, rather than by a abiding number. Growth that occurs at a constant percent each unit of time is called exponential growth.

Nosotros can expect at growth for each site to sympathize the deviation. The table compares the number of users for each site for 12 months. The table shows the calculations for the outset 4 months but, just uses the same adding process to complete the residual of the 12 months.

Month	Users at Site A	Users at Site B
0	\(10000\)	\(10000\)
1	\(10000 + 1500 = 11500\)	\(\begin{aligned} 10000+&10 \% \text { of } 10000 \\ =& 10000+0.10(10000) \\ =& 10000(1.10)=11000 \terminate{aligned}\)
2	\(11500 + 1500 = 13000\)	\(\begin{aligned} 11000+&x \% \text { of } 11000 & \\ =&11000+0.10(11000) \\ =&11000(ane.10)=12100 \stop{aligned}\)
3	\(13000 + 1500 = 14500\)	\(\begin{aligned} 12100+&x \% \text { of } 12100 & \\ =&12100+0.ten(12100) \\ =&12100(1.x)=13310 \end{aligned}\)
four	\(14500 + 1500 = 16000\)	\(\begin{aligned} 13310+&x \% \text { of } 13310 \\ =&13310+0.10(13310) \\ =&13310(i.10)=14641 \end{aligned}\)
5	\(17500\)	\(16105\)
vi	\(19000\)	\(17716\)
7	\(20500\)	\(19487\)
viii	\(22000\)	\(21436\)
9	\(23500\)	\(23579\)
10	\(25000\)	\(25937\)
11	\(26500\)	\(28531\)
12	\(28000\)	\(31384\)

For Site B, we tin can re-express the calculations to assistance us observe the patterns and develop a formula for the number of users after 10 months.

• Month ane: \(y = 10000(1.i) = 11000\)
• Month 2: \(y = 11000(1.1) = 10000(ane.one)(i.1)=\mathbf{10000(one.1)^2}= 12100\)
• Month 3: \(y = 12100(1.1) = 10000(ane.i)^2 (one.i)=\mathbf{10000(1.1)^3}= 13310\)
• Calendar month 4: \(y = 13310(i.1) = 10000(1.1)^iii (1.one)=\mathbf{10000(1.1)^4}= 14641\)

Past looking at the patterns in the calculations for months two, 3, and four, we can generalize the formula. After \(x\) months, the number of users \(y\) is given by the function \(\mathbf{y = 10000(1.i)^ten}\)

Example \(\PageIndex{1}\)

Make up one's mind whether each of the post-obit statements represent exponential growth or linear growth.

1. The population of a certain boondocks has been increasing by two.four% over each of the last x years.
2. The population of a certain town has been increasing by 1,000 people over each of the last 10 years.
3. The number of bacterial cells increases by a factor of \(\dfrac{3}{2}\) every 24 hours.

Solution

a.  Since the population has been increasing past a constant per centum for each unit of time, this is an instance of exponential growth.

b.  Since the population has been increasing by a constant number for each unit of time, this is an example of linear growth.

c.  Since the number of cells has been increasing by a constant percent \( (\dfrac{three}{2}=150\%) \) for each unit of measurement of time, this is an example of exponential growth.

Using Exponential Functions to Model Growth and Decay

In exponential growth, the value of the dependent variable \(y\) increases at a constant percentage rate equally the value of the independent variable (\(x\) or \(t\)) increases. Examples of exponential growth functions include:

• the number of residents of a urban center or nation that grows at a constant per centum charge per unit.
• the amount of coin in a depository financial institution business relationship that earns involvement if money is deposited at a single point in time and left in the bank to compound without any withdrawals.

In exponential decay, the value of the dependent variable y decreases at a constant percentage charge per unit every bit the value of the independent variable (\(ten\) or \(t\)) increases. Examples of exponential disuse functions include:

• value of a car or equipment that depreciates at a constant per centum charge per unit over time
• the amount a drug that all the same remains in the body equally time passes after it is ingested
• the corporeality of radioactive cloth remaining over time as a radioactive substance decays.

Exponential functions often model quantities as a role of time; thus nosotros oftentimes use the letter of the alphabet \(t\) as the independent variable instead of \(x\).

The tabular array compares exponential growth and exponential decay functions:

Exponential Growth	Exponential Decay
Quantity grows by a constant per centum per unit of time	Quantity decreases past a constant percent per unit of time
\(\mathbf{y=ab^x}\) \(a\) is a positive number representing the initial value of the function when \(ten = 0\) \(b\) is a real number that is greater than i: \(b > 1\) the growth charge per unit \(r\) is a positive number, \(r > 0\) where \(b = 1+ r\) (so that \(r = b-1\))	\(\mathbf{y=ab^x}\) \(a\) is a positive number representing the initial value of the function when \(x = 0\) \(b\) is a real number that is between 0 and i: \(0 < b < 1\) the decay rate \(r\) is a negative number, \(r < 0\) where \(b = i+ r\) (so that \(r = b-1\))

In general, the domain of exponential functions is the set of all real numbers. The range of an exponential growth or disuse part is the ready of all positive real numbers.

In near applications, the contained variable, \(x\) or \(t\), represents time. When the independent variable represents time, we may cull to restrict the domain so that independent variable can take just not-negative values in society for the awarding to make sense. If we restrict the domain, then the range is besides restricted also.

• For an exponential growth function \(y=ab^x\) with \(b>1\) and \(a > 0\), if nosotros restrict the domain and then that \(x ≥ 0\), and so the range is \(y ≥ a\).
• For an exponential decay part \(y=ab^x\) with \(0<b<1\) and \(a > 0\), if we restrict the domain so that \(ten ≥ 0\), then the range is \(0 < y ≤ a\).

Example \(\PageIndex{2}\)

Consider the growth models for social media sites A and B, where \(x\) = number of months since the site was started and \(y\) = number of users. The number of users for Site A follows the linear growth model:

\[y = 10000+1500x \nonumber.\]

The number of users for Site B follows the exponential growth model:

\[y=10000(ane.1^ten) \nonumber\]

For each site, use the function to calculate the number of users at the stop of the first year, to verify the values in the table. And so use the functions to predict the number of users afterward xxx months.

Solution

Since \(x\) is measured in months, then \(ten = 12\) at the stop of i year.

Linear Growth Model:

When \(x = 12\) months, and so \(y = 10000 + 1500(12) = 28,000\) users
When \(x = 30\) months, then \(y = 10000 + 1500(30) = 55,000\) users

Exponential Growth Model:

When \(x = 12\) months, and then \(y = 10000(1.ane^{12}) = 31,384\) users
When \(10 = 30\) months, then \(y = 10000(1.1^{thirty}) =174,494\) users

Nosotros see that as \(ten\), the number of months, gets larger, the exponential growth function grows large faster than the linear office (fifty-fifty though in Case \(\PageIndex{2}\) the linear office initially grew faster). This is an important characteristic of exponential growth: exponential growth functions ever grow faster and larger in the long run than linear growth functions.

Information technology is helpful to use function note, writing \(y = f(t) = ab^t\), to specify the value of \(t\) at which the function is evaluated.

Example \(\PageIndex{iii}\)

A forest has a population of 2000 squirrels that is increasing at the rate of iii% per year. Let \(t\) = number of years and \(y = f(t) =\) number of squirrels at time \(t\).

1. Notice the exponential growth office that models the number of squirrels in the forest at the cease of \(t\) years.
2. Use the part to find the number of squirrels subsequently 5 years and afterward x years

Solution

a. The exponential growth function is \(y = f(t) = ab^t\), where \(a = 2000\) considering the initial population is 2000 squirrels

The annual growth rate is three% per twelvemonth, stated in the problem. We will limited this in decimal form equally \(r = 0.03\)

Then \(b = i+r = 1+0.03 = 1.03\)

Answer: The exponential growth function is \(y = f(t) = 2000(i.03)^t\)

b. After 5 years, the squirrel population is \(y = f(5) = 2000(1.03)^5 \approx 2319\) squirrels

After 10 years, the squirrel population is \(y = f(10) = 2000(i.03)^{10} \approx 2688\) squirrels

Example \(\PageIndex{4}\)

A large lake has a population of yard frogs. Unfortunately the frog population is decreasing at the charge per unit of five% per year. Let \(t\) = number of years and \(y\) = \(g(t)\) = the number of frogs in the lake at fourth dimension \(t\).

1. Find the exponential decay role that models the population of frogs.
2. Calculate the size of the frog population after 10 years.

Solution

a. The exponential decay function is \(y = grand(t) = ab^t\), where \(a = m\) considering the initial population is 1000 frogs

The annual decay charge per unit is 5% per year, stated in the problem. The words decrease and decay indicated that \(r\) is negative. We limited this as \(r = -0.05\) in decimal form.

Then, \(b = 1+ r = 1+ (-0.05) = 0.95\)

Answer: The exponential decay function is: \(y = yard(t) = yard(0.95)^t\)

b. After 10 years, the frog population is \(y = g(ten) = k(0.95)^{10} \approx 599\) frogs

Example \(\PageIndex{v}\)

A population of bacteria is given by the function \(y = f(t) = 100(2)^t\), where \(t\) is time measured in hours and \(y\) is the number of bacteria in the population.

1. What is the initial population?
2. What happens to the population in the first hour?
3. How long does it take for the population to reach 800 bacteria?

Solution

a. The initial population is 100 leaner. We know this because \(a = 100\) and because at time \(t = 0\), then \(f(0) = 100(2)^0 = 100(1)=100\)

b. At the end of 1 hour, the population is \(y = f(1) = 100(two)^1 = 100(two)=200\) bacteria.
The population has doubled during the first hour.

c. Nosotros need to find the time \(t\) at which \(f(t) = 800\). Substitute 800 as the value of \(y\):

\[\begin{array}{fifty}
y=f(t)=100\left(ii\right)^{t} \\
800=100\left(2\right)^{t}
\cease{array}\nonumber\]

Divide both sides by 100 to isolate the exponential expression on the i side

\[eight=1\left(two\right)^{\mathrm{t}} \nonumber\]

8 = 2³, so it takes \(t = three\) hours for the population to reach 800 bacteria.

2 important notes about Instance \(\PageIndex{5}\):

• In solving \(8 = 2^t\), nosotros "knew" that \(t\) is 3. But we usually tin not know the value of the variable just past looking at the equation. Later nosotros will apply logarithms to solve equations that have the variable in the exponent.
• To solve \(800 = 100(2)^t\), nosotros divided both sides by 100 to isolate the exponential expression \(ii^t\). Nosotros can not multiply 100 by 2. The exponent applies only to the quantity immediately before it, so the exponent t applies only to the base of 2.

Comparing Linear, Exponential and Polynomial Functions

To place the type of role from its formula, nosotros need to carefully note the position that the variable occupies in the formula.

A linear function can exist written in the form \(\mathbf{y=a x+b}\)

As we studied in chapter one, at that place are other forms in which linear equations can be written, only linear functions can all be rearranged to have grade \(y = mx + b\).

An exponential office has grade \(\mathbf{y=ab^ten}\)

The variable \(\mathbf{10}\) is in the exponent. The base of operations \(b\) is a positive number.

• If \(b>1\), the function represents exponential growth.
• If \(0 < b < 1\), the office represents exponential decay

A polynomial function has form \(\mathbf{y=ax^P+bx^{P-ane}+cx^{P-2}+...}\)

The variable \(\mathbf{x}\) is in the base. The exponent \(p\) is a non-naught number, and the exponents subtract until the final exponent is naught.

We compare three functions, using increasing x values:

• linear function \(y = f(x) = 2x\)
• exponential function \(y = g(x) = 2^10\)
• polynomial function \(y = h(x) = x^two\)

\(\mathbf{x}\)	\(\mathbf{y = f(x) =2x}\)	\(\mathbf{y = k(x) =two^x}\)	\(\mathbf{y= h(x) =x^ii}\)
0	0	ane	0
1	two	ii	one
ii	4	4	4
3	6	eight	9
4	8	16	16
5	10	32	25
6	12	64	36
10	twenty	1024	100
Type of function	Linear \(y = mx+b\)	Exponential \(y = ab^x\)	Polynomial\(y = cx^P\)
How to recognize equation for this type of office.	all terms are first degree; \(m\) is slope; \(b\) is the \(y\) intercept	base is a number \(b>0\); the variable is in the exponent	variable is in the base; exponent is a number \(\mathrm{p} \neq 0\)
	For equal intervals of modify in \(x\), \(y\) increases by a abiding amount	For equal intervals of alter in \(x\), \(y\) increases by a constant ratio

For the functions in the previous tabular array: linear office \(y = f(ten) = 2x\), exponential function \(y = g(x) = ii^x\), and polynomial role \(y = h(x) = x^2\), if nosotros restrict the domain to \(x ≥ 0\) only, then all these functions are growth functions. When \(10 ≥ 0\), the value of \(y\) increases equally the value of \(x\) increases.

The exponential growth role grows big faster than the linear and polynomial functions, as \(x\) gets large. This is e'er true of exponential growth functions, every bit \(ten\) gets large enough.

Case \(\PageIndex{vi}\)

Allocate the functions below as exponential, linear, or polynomial functions.

1. \(y=10x^three\)
2. \(y=-200-30x\)
3. \(y=m(1.05)^x\)
4. \(y=500(0.75)^x\)
5. \(y=-0.2x^iv\)
6. \(y=5x-1\)
7. \(y=6x^2+3x\)

Solution:

The exponential functions are

c. \(y=thousand(1.05)^x\) The variable is in the exponent; the base of operations is the number \(b = one.05\)

d. \(y=500(0.75)^x\) The variable is in the exponent; the base is the number \(b = 0.75\)

The linear functions are

b. \(y=-200-30x\)

f. \(y=5x-1\)

The polynomial functions are

a. \(y=10x^iii\) The variable is the base of operations; the exponent is a fixed number, \(p=three\).

e. \(y=-0.2x^four\) The variable is the base; the exponent is a number, \(p=4\).

g. \(y=6x^2+3x\) The variable is the base of operations; the exponent is a number, \(p = 2\).

NATURAL BASE: east

The number e is often used as the base of an exponential function. e is chosen the natural base.

e is approximately 2.71828

e is an irrational number with an space number of decimals; the decimal blueprint never repeats.  Department viii.two includes an example that shows how the value of e is developed and why this number is mathematically of import.

When due east is the base in an exponential growth or decay function, it is referred to as continuous growth or continuous decay. We will apply east in Chapter viii in financial calculations when nosotros examine interest that compounds continuously.

Any exponential function can be written in the grade \(\mathbf{y = ae^{kx}}\)

\(\mathbf{yard}\) is called the continuous growth or decay rate.

• If \(k > 0\), the role represents exponential growth
• If \(k< 0\), the part represents exponential disuse

\(\mathbf{a}\) is the initial value

We tin can rewrite the office in the course \(\mathbf{y = ab^ten}\), where \(\mathbf{b=e^1000}\)

In general, if we know one form of the equation, we tin can notice the other forms. For now, we take not yet covered the skills to discover \(k\) when we know \(b\). Subsequently we learn about logarithms afterward in this chapter, we will find \(one thousand\) using natural log: \(yard = \ln b\).

The table beneath summarizes the forms of exponential growth and decay functions.

	y = ab x	y = a(i+r) x	y = ae kx , g ≠ 0
Initial value	a>0	a>0	a>0
Relationship between b, r, k	b > 0	b=ane+ r	b = e k and k = ln b
Growth	b > 1	r > 0	k > 0
Decay	0 < b < 1	r < 0	k < 0

Example \(\PageIndex{seven}\)

The value of houses in a city are increasing at a continuous growth rate of half dozen% per twelvemonth. For a house that currently costs $400,000:

1. Write the exponential growth function in the form \(y=ae^{kx}\).
2. What would be the value of this firm iv years from now?
3. Rewrite the exponential growth office in the grade \(y=ab^x\).
4. Detect and interpret \(r\).

Solution

a. The initial value of the firm is \(a\) = $400000

The trouble states that the continuous growth rate is 6% per twelvemonth, and then \(grand\) = 0.06

The growth function is : \(y=400000e^{0.06x}\)

b. After 4 years, the value of the firm is \(y=400000e^{0.06 (iv)}\) = $508,500.

c. To rewrite \(y=400000e^{0.06x}\) in the form \(y = ab^ten\), we use the fact that \(b=e^k\).

\[\begin{assortment}{fifty}
\mathrm{b}=due east^{0.06} \\
\mathrm{b}=1.06183657 \approx 1.0618 \\
\mathrm{y}=400000(i.0618)^{\mathrm{ten}}
\finish{assortment}\nonumber\]

d. To detect \(r\), we apply the fact that \(b=1+ r\)

\[\begin{assortment}{l}
\mathrm{b}=1.0618 \\
1+\mathrm{r}=ane.0618 \\
\mathrm{r}=0.0618
\end{array} \nonumber \]

The value of the house is increasing at an annual rate of half dozen.18%.

Example \(\PageIndex{viii}\)

Suppose that the value of a certain model of new auto decreases at a continuous decay rate of 8% per twelvemonth. For a car that costs $xx,000 when new:

1. Write the exponential decay part in the form \(y=ae^{kx}\).
2. What would be the value of this car 5 years from now?
3. Rewrite the exponential decay function in the grade \(y=ab^ten\).
4. Find and interpret \(r\).

Solution

a. The initial value of the car is \(a\) = $20000

The trouble states that the continuous disuse rate is viii% per twelvemonth, so \(k\) = -0.08

The growth function is : \(y=20000e^{-0.08x}\)

b. Later on five years, the value of the automobile is \(y=20000 due east^{-0.08 (5)}\) = $xiii,406.40.

c. To rewrite \(y=20000e^{-0.08x}\) in the grade \(y=ab^ten\), nosotros utilise the fact that \(b=e^k\).

\[\brainstorm{array}{fifty}
\mathrm{b}=east^{-0.08} \\
\mathrm{b}=0.9231163464 \approx 0.9231 \\
\mathrm{y}=20000(0.9231)^{\mathrm{ten}}
\stop{array} \nonumber \]

d. To discover \(r\), we use the fact that \(b=1+ r\)

\[\brainstorm{array}{l}
\mathrm{b}=0.9231 \\
\mathrm{50}+\mathrm{r}=0.9231 \\
\mathrm{r}=0.9231-1=-0.0769
\end{array} \nonumber\]

The value of the car is decreasing at an annual rate of vii.69%.

thomasonvorcy1981.blogspot.com

Source: https://math.libretexts.org/Courses/Community_College_of_Denver/MAT_123_Finite_Mathematics/07:_Exponential_and_Logarithmic_Functions/7.01:_Exponential_Growth_and_Decay_Models

Share this post